MIT Strategic Engineering

Matlab Tools for Network Analysis (2006-2011)

This toolbox was first written in 2006. The last version, posted here, is from November 2011. These routines are useful for someone who wants to start hands-on work with networks fairly quickly, explore simple graph statistics, distributions, simple visualization and compute common network theory metrics. The code is not object-oriented, and should be easy to use, read and improve upon. There is some overlap with the grTheory toolbox and the MatlabBGL library published on Matlab Central. Different authorship is indicated in the header. No code is perfect so please contact gergana at alum dot mit.edu if you notice errors or have pointers to better routines.

This code is published under the BSD license. The license text is also available at the end of this page.

Current version

The new and current version of this code is available in Octave (GNU Octave Version 3.4.0 and Gnuplot 4.2.5) here. Some parts of the code are restructured and updated. All functions are generally better documented. The Octave toolbox also includes a manual with background information and examples.

Archived Version (frozen Nov. 2011)

The code is classified by functionality as follows (121 routines total, last version Nov 6, 2011). All functions can be downloaded here.

Basic network routines (17)

getNodes.m - return the list of nodes for varying graph representations;
getEdges.m - return the list of edges for varying graph representations;
numnodes.m - number of vertices/nodes in the network;
numedges.m - number of edges/links in the network;
link_density.m - the density of links of the graph;
selfloops.m - number of selfloops, i.e. nodes connected to themselves;
multiedges.m - number of arcs (i,j) with multiple edges across them;
average_degree.m - the average degree (# links) across all nodes;
num_conn_comp.m - number of connected components (using algebraic connectivity);
find_conn_comp.m - the number of connected components in an undirected graph;
giant_component.m - extract the giant component only (undirected graph);
tarjan.m - find the strongly connected components in a directed graph;
graph_complement.m - the complement graph;
graph_dual.m - the graph dual (or line graph, adjoint graph);
subgraph.m - return the subgraph adjacency given the graph and the subgraph nodes;
leaf_nodes.m - nodes connected to only one other node;
leaf_edges.m - edges with only one adjacent edge;

Diagnostics (11)

issimple.m - check whether the graph has selfloops and multiple edges;
isdirected.m - directed or undirected graph (right now uses issymmetric.m);
issymmetric.m - check whether a matrix is symmetric;
isconnected.m - check whether a graph is connected;
isweighted.m - determine whether the graph has weighted links;
isregular.m - check whether it's a regular graph;
iscomplete.m - check whether the graph is complete;
iseulerian.m - find out whether it's an eulerian graph;
istree.m - check whether the graph is a tree;
isgraphic.m - check whether a sequence of numbers is graphic;
isbipartite.m - check whether a graph is bipartite;

Conversion routines (14)

adj2adjL.m, (adjL2adj.m) - convert an adjacency matrix to an adjacency list;
adj2edgeL.m, (edgeL2adj.m) - convert an adjacency matrix to an edge list;
adj2inc.m, (inc2adj.m) - convert adjacency matrix to incidence matrix and vice-versa;
adj2str.m, (str2adj.m) - convert adjacency matrix to a string graph representation;
adjL2edgeL.m, (edgeL2adjL.m) - convert adjacency list to edge list;
inc2edgeL.m - convert incidence matrix to an edge list;
adj2simple.m - Remove selfloops and multiedges from an adjacency matrix;
edgeL2simple.m - remove selfloops and multiedges from an edge list;
add_edge_weights.m - adding edges that occur multiple times in an edgelist;

Centrality measures & Distributions (15)

degrees.m - total degree, in- and out-degree sequence of an arbitrary graph;
rewire.m - degree-preserving rewiring;
rewire_assort.m - degree-preserving rewiring with increasing assortativity;
rewire_disassort.m - degree-preserving rewiring with decreasing assortativity;
(for degree preserving rewiring, see also code by Maslov);
ave_neighbor_deg.m - the average degree of neighboring nodes for every vertex;
closeness.m - computes the closeness centrality for all vertices;
node_betweenness.m - node betweenness, (number of shortest paths definition);
node_betweenness.m - a faster node betweenness algorithm;
edge_betweenness.m - edge betweenness, (number of shortest paths definition);
eigencentrality.m - eigenvector corresponding to the largest eigenvalue;
clust_coeff.m - two clustering coefficients: based on loops and local clustering;
weighted_clust_coeff.m - weighted clustering coefficient;
pearson.m - pearson degree correlation;
rich_club_metric.m
s_metric.m - the sum of products of nodal degrees across all edges;

Spectral properties (6)

laplacian_matrix.m - the Laplacian of the graph: degree matrix minus the adjacency;
graph_spectrum.m - the sorted eigenvalues of the Laplacian;
algebraic_connectivity.m - the second smallest eigenvalue of the Laplacian;
fiedler_vector.m - the eigenvector corresponding to the algebraic connectivity;
eigencentrality.m - see Centrality measures & Distributions
graph_energy.m

Distances (12)

simple_dijkstra.m - simple Dijkstra, does not remember the path;
dijkstra.m - Dijkstra which also returns the shortest paths;
shortest_pathDP.m - shortest path algorithm using dynamic programming;
kneighbors.m - returns the indices of all neighbors k links away (for a given node);
kmin_neighbors.m - indices of all neighbors minimum k links away (for a given node);
diameter.m - the longest shortest path in the graph;
ave_path_length.m - the average shortest path in the graph;
smooth_diameter.m - a smoothed definition of diameter (effective diameter);
closeness.m - see Centrality measures & Distributions;
vertex_eccentricity.m - the maximum distance to any other vertex;
graph_radius.m - the minimum vertex eccentricity;
distance_distribution.m - fraction of nodes at a given distance;

Comparing graphs (1)

graph_similarity.m - hubs and authorities based graph similarity matrix;

Modularity (6)

spectral_partitioning.m simple spectral partitioning;
Newman-Girvan algorithm for community finding;
Newman eigenvector modularity routine;
newman_comm_fast.m faster community finding (Newman, 2003/4);
modularity_metric.m - as defined in Newman/Girvan above;
louvain_community_finding.m

Example of Spectral Partitioning

Motifs (4)

loops3.m - count all loops of size 3 in the graph;
loops4.m - returns all loops of size 4;
num_loops.m - number of independent loops;
num_star_motifs.m - number of star motifs of given size;

Building graphs (16)

random_graph.m - generate a random graph adjacency matrix using various models;

random_graph(n) - Erdos-Renyi graph with n nodes and probability of attachment 0.5;
random_graph(n,p) - Erdos-Renyi graph with n nodes and probability of attachment p;
random_graph(n,[ ],E) - random graph with E number of edges;
random_graph(n,[ ],[ ],distribution) - nodal degrees are drawn from a particular distribution (uniform, normal, binomial, exponential);
random_graph(n,[ ],[ ],'sequence',deg_seq) - the degrees match a given sequence;
random_directed_graph.m - simple random directed graph routine;
random_modular_graph.m - random graph with modules;
graph_from_degree_sequence.m - build deterministic graph given the nodal degrees;
canonical_nets.m - simple graphs such as trees, lattices and hierarchical trees;
kregular.m - simple routine for building k-regular graphs;
PriceModel.m - Price's citations growth model;
preferential_attachment.m - preferential attachment graph;
exponential_growth_model.m;
master_equation.m - a generalization of the degree-based random growth models;
newmangastner.m - Newman-Gastner spatial distribution growth model;
fabrikant_model.m - another spatial distribution growth model;
DoddsWattsSabel.m - building randomized hierarchies, the Dodds-Watts-Sabel model;
s-max graph - graph with the same degree sequence but maximum s-metric;
forest fire model ;

nested hierarchies model by Sales-Pardo et al, 2007;

Hex Lattice

Random Modular Graph

Newman Gastner Example

Drawing graphs (13)

pdf_cdf_rank.m - pdf, cdf and rank distributions of a given sequence;
adj2pajek.m, (pajek2adj.m) - adjacency matrix to Pajek format: output .net file;
edgeL2pajek.m, (pajek2edgeL.m) - edge list to Pajek format: output .net file;
pajek2xyz.m - Extract node x,y,z coordinates from a Pajek .net file;
el2geom.m - plot an edge list geographically with color-coding of edge weights;
edgeL2cyto.m - convert edge list to Cytoscape text input;
adj2dl.m - adjacency to UCINET format; by D. Whitney;
edgelist2dl.m - edge list to UCINET format; by D. Whitney;
draw_circ_graph.m - draw a graph with all nodes in a circle, ordered by degree;
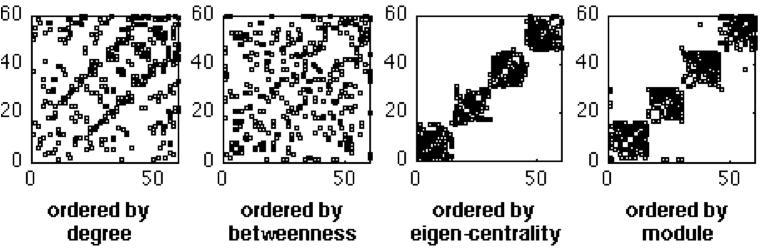
dot_matrix_plot.m - sparsity plots with nodes sorted by degree, betw-ness, modularity;
radial_plot.m - best for trees and sparse graphs;

Dot Matrix Example

Circle Draw Example

Continental US

Radial Plot Example

Auxiliary (8)

symmetrize.m - symmetrize a matrix;
symmetrize_edgeL.m - symmetrize an edge list (make it undirected);
num_conn_triples.m - the number of connected triples of nodes;
purge.m - remove elements from a list, while preserving the order;
min_span_tree.m - construct a minimum spanning tree given the adjacency matrix;
BFS.m - breadth-first tree;
sort nodes by the sum of neighbor degrees;
sort nodes by the maximum neighbor degree;

Publications

Bounova, G., de Weck, O.L. "Overview of metrics and their correlation patterns for multiple-metric topology analysis on heterogeneous graph ensembles", Phys. Rev. E 85, 016117 (2012).

Copyright (c) 2011, Massachusetts Institute of Technology.
All rights reserved.
Redistribution and use in source and binary forms, with or without modification, are permitted provided that the following conditions are met:

Redistributions of source code must retain the above copyright notice, this list of conditions and the following disclaimer.
Redistributions in binary form must reproduce the above copyright notice, this list of conditions and the following disclaimer in the documentation and/or other materials provided with the distribution.
Neither the name of the Massachusetts Institute of Technology nor the names of its contributors may be used to endorse or promote products derived from this software without specific prior written permission.

THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT HOLDER OR CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.